Dans « Why are past, present, and future our only options?« , Dave Goldberg traite de la « question bête » d’un lecteur de son livre[1] qui se demande à quoi ressemblerait l’univers si le temps avait plus d’une dimension, et plus généralement, si la vie serait imaginable dans un univers à N≠3 dimensions. Voici quelques idées qu’il y développe, additionnées des miennes sur ce sujet.
La vie dans un espace à 2 dimensions (+1 temps) a été imaginée dès 1884 dans « Flatland » [2], une allégorie purement géométrique dont a été tiré un film en 2007 :
Un siècle plus tard, A.K. Dewdney a traité de manière beaucoup plus « scientifique » la physique, la chimie et la biologie dans « Le Planivers » [3], répondant au passage à une objection de Dave Goldberg : oui, il est possible de croiser deux fils dans le Planivers, comme indiqué ici, donc de réaliser des ordinateurs en 2D, comme le montre également le « Jeu de la Vie » qui est une machine « Turing complète »
Un univers à N=1 dimension (+1 temps) n’est pas imaginable en physique, mais du point de vue artistique j’aime beaucoup « la Linea » de mon enfance, un dessin animé minimaliste en « 1½ D » avec interventions ponctuelles d’un Créateur tridimensionnel :
A propos d’un univers à N=4 dimensions spatiales (+1 temps toujours), Dave Goldberg mentionne un fait que je n’avais pas réalisé : l’action des forces n’y diminue pas comme l’inverse du carré de la distance comme dans notre univers, mais comme l’inverse du cube de la distance. Ceci fait notamment qu’aucune planète à 4 dimensions ne peut décrire une orbite stable autour de son soleil hypersphérique. Le problème ne s’arrangeant pas en augmentant les dimensions il faut se rendre à l’évidence : un univers « fertile », où la complexité peut se développer jusqu’à permettre des formes de vie ne peut avoir que N=3 dimensions, ou à la rigueur 2.
Plus une seule dimension de temps, toujours. Quelle que soit la « nature du temps » on n’y coupe pas : au niveau macroscopique bien décrit par la relativité d’Albert, le temps est décrit par une dimension imaginaire, au sens mathématique des nombres complexes. Evidemment, sans temps un univers serait désespérément statique et sans intérêt.
Mais peut-on imaginer un temps à plus d’une dimension ? Mathématiquement ça ne pose pas trop de problèmes et les caractéristiques de tels univers ont été étudiées, notamment par Max Tegmark. Son très intéressant article [4] soulève la difficulté majeure posée par un univers à plusieurs dimensions de temps :
Si un observateur est capable d’utiliser sa conscience de soi et des capacités de traitement de l’information, les lois de la physique doivent être telles qu’il puisse faire au moins certaines prédictions. Plus précisément, au sein du cadre d’une théorie des champs, en mesurant diverses valeurs de champ à proximité, il faut qu’il ait la possibilité de calculer les valeurs de champ à certains points plus éloignés de l’espace-temps (ceux se trouvant le long de la ligne de son monde à venir sont particulièrement utiles) avec une marge d’erreur finie. Si ce type de causalité bien définie était absente, alors non seulement il n’y aurait aucune raison pour que cet observateur ait une conscience de soi, mais il semble très peu probable que des systèmes de traitement de l’information tels que les ordinateurs ou le cerveau puisse exister.
Or justement cette prédictibilité n’apparaît que si les équations de champ suivent des équations différentielles partielles « hyperboliques ». Et Tegmark montre que ceci n’est le cas que dans les univers à une seule dimension de temps ou une seule dimension d’espace. S’il y en a plus, l’univers devient totalement imprévisible. Avec un temps à deux dimensions, il est par exemple impossible de donner un rendez-vous à quelqu’un, car si nous contrôlons nos déplacements dans l’espace et pouvons éventuellement les moduler de façon à nous retrouver à un certain moment t1 selon le « temps1 » à l’endroit convenu, nous n’aurions pas le moyen de gérer simultanément le « temps2 » : l’autre personne suivant une trajectoire dans l’espace-temps différente n’aurait aucun moyen d’arriver au rendez-vous à la fois à la même position spatiale et au au même temps (t1,t2)
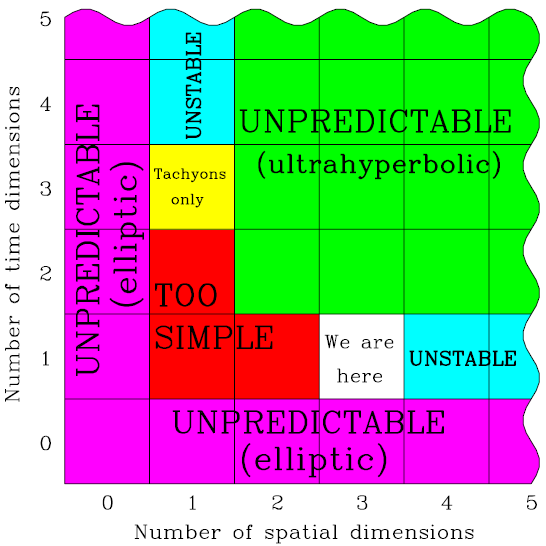
Le tableau suivant résume les caractéristiques des univers selon leurs dimensions spatiales et temporelles selon Tegmark:
Notre univers n’est donc pas le résultat d’une expérience menée par des êtres à 4 dimensions, ou de dieux pour lesquels notre temps ne serait qu’une dimension parmi beaucoup d’autres. Nous ne sommes pas manipulés comme « La Linea », ça soulage…
Le tableau exhibe aussi une jolie symétrie entre entre dimensions spatiales et dimensions temporelles, ce qui laisse espérer un autres univers intéressant, notre « symétrique » à une dimension spatiale et « temps cubique ». Dans cet univers, la physique des particules n’autorise que l’existence de tachyons, des particules très hypothétiques dans notre univers mais liées à la théorie des cordes, laquelle postule l’existence de dimensions « bouclées » à très petite échelle en plus des dimensions spatiales. Dès qu’on vérifie leur existence expérimentalement j’écris un article là dessus, promis.
Références:
- Dave Goldberg, Jeff Blomquist "A User's Guide to the Universe: Surviving the perils of black holes, time paradoxes, and quantum uncertainty" (2010) Wiley ISBN:9780470496510 WorldCat Google Books
- Edwin Abbott Abbott "Flatland: A Romance of Many Dimensions" (1885) Roberts brothers ISBN: WorldCat Google Books (texte intégral en français en pdf)
- A.K. Dewdney "le Planivers: Contact informatique avec un monde à deux dimensions" (1985) Londreys ISBN:9782904184208 WorldCat Google Books
- [altmetric doi= »10.1088/0264-9381/14/4/002″ float= »right »]Max Tegmark, « On the dimensionality of spacetime« , 1997, arXiv:gr-qc/9702052v2, DOI 10.1088/0264-9381/14/4/002




23 commentaires sur “Pourquoi 3 dimensions + 1 temps ?”
Le temps et les dimensions spatiales ont une différence de nature. Macroscopiquement on doit considérer le temps comme une dimension imaginaire ( voir https://drgoulu.com/2007/02/07/le-temps-une-4eme-dimension-imaginaire/ )
Concernant l’utilisation du mot « quantique » en dehors de la physique, je suis pour le moins circonspect.. Les phénomènes quantiques étant très peu intuitifs et conformes à notre expérience quotidienne, j’ai souvent l’impression qu’ils sont exploités par certains pour emberlificoter les choses plutôt que de les éclairer (sans préjuger du site que vous indiquez, que je n’ai parcouru qu’en diagonale).
Cela dit on peut tout de même tirer des parallèles, voir par exemple http://www.rtflash.fr/cerveau-l-homme-flirte-avec-physique-quantique/article
Cette analyse postule que toutes les dimensions opèrent simultanément. Or on pourrait très bien envisager des univers, où les dimensions supplémentaires opèrent pour certaines catégories de phénomènes, ou à certaines échelles.
Un espace à 2 dimensions, c’est à dire un plan, n’empêche pas l’existence d’une droite (1 dimension) ou les mouvements sont plus restreints, mais le plan admet la possibilité d’existence d’une infinité de droites.
Oui effectivement l’étude se limite aux espaces métriques (dans lesquels on peut définir une « distance » entre deux points), car c’est cette norme qui définit le type des équations aux différentielles partielles qui régiraient ces univers.
La notion de dimensions enroulées qui agiraient à toute petite échelle a été proposée notamment dans le cadre de la théorie des cordes mais hélas cette théorie a du plomb dans l’aile notamment depuis les dernières expériences au LHC du CERN ne l’ont pas confirmée… Si j’ai bien compris, lors de certaines expériences de l’énergie aurait du être perdue dans des dimensions cachées, et/ou certaines particules exotiques auraient du être détectées. Donc pour l’instant, ces dimensions cachées n’existent que sous forme de traces blanches sur le tableau noir des matheux…
Mais effectivement on peut se demander quelle serait leur influence si elles existaient. Il me semble au pif que ça ne rendrait pas les équations d’un espace à N dimensions macroscopiques plus simples, plus intégrables, donc plus prévisibles. Dans le meilleur des cas ces dimensions passeraient inaperçues à notre échelle. (j’ai essayé de comprendre https://fr.wikipedia.org/wiki/Réduction_dimensionnelle , mais pas pu…)
Je découvre à l’instant la proposition de Itzhak Bars d’ajouter une deuxième dimension de temps « enroulée » pour sauver la théorie des cordes http://www.futura-sciences.com/magazines/matiere/infos/actu/d/physique-theorie-m-pourrait-necessiter-deux-dimensions-temporelles-11878/ . Je n’en trouve plus trace après 2007, il y a du y avoir une bulle…
Je me demande s’il n’existe pas déjà des dimensions supplémentaires que nous n’identifions pas encore comme telle :
Par exemple ne peut-on considérer l’espace de Hilbert quantique comme une dimension supplémentaire ?
Cette dimension au sein de laquelle se produisent les interactions quantiques permet la mise en communication de régions éloignées de l’espace, par le phénomène EPR.
D’un point de vue topologique cela revient à considérer les interactions de type EPR comme de pont ER :
autrement dit des trous de ver.
En tout cas, une chose est sûre, l’hypothèse « EPR = ER » est prise très au sérieux.
http://www.pourlascience.fr/ewb_pages/a/actu-un-lien-entre-intrication-quantique-et-trous-de-ver-32465.php
Peut-être bien qu’il existe des univers parallèles, ou inclus dans le nôtre, ou dans lesquels le nôtre est inclus. Les maths permettent plein de choses merveilleuses… La physique est un peu plus restrictive, mais ce qui me paraît intéressant dans cet article ce sont les conséquences d’un univers différent sur la vie. D’après la forme générale des équations de champ bien notre univers combine ce qu’il faut de prévisibilité avec ce qu’il faut d’imprévisibilité pour que des structures aussi complexes que notre cerveau puissent émerger. Les univers qui n’ont pas 3+1 dimensions sont probablement stériles. Dommage, moi j’aime bien le Planivers…
Je découvre bien tard ce très bon article.
Toutefois pas convaincu que l’on ne puisse pas être dans un univers 3D + 1.000001T.
Je m’explique: un univers 2T, mais où se mouvoir dans le 2ème T soit très difficile et prédictible. Par exemple seulement si on a une très grande énergie cinétique.
Dans la vie de tout les jours, on aurait l’impression d’être tous à même temps, mais en fait tous légèrement décalés.
En pondant un commentaire pour http://algorythmes.blogspot.com/2013/07/livre-dete-flatland-dedwin-abbott.html j’ai accidentellement retrouvé sur mon premier site, toujours perdu dans les limbes d’internet, la page http://goulus.tripod.com/science/planivers.htm avec le texte d’un de mes articles publié dans le journal des étudiants du Collège de St-Maurice en 1980 sous le titre « DIVERTISSEMENT MATHEMATIQUE »)
Le divertissement que je vous propose est issu d’un article de Martin Gardner paru dans le numéro d’août 1980 du journal « Pour la science’,édition française du respectable »Scientific American » dont je vous livre quelques extraits destinés à vous exposer le problème.
« Pour autant que nous le sachions, le seul univers existant est celui dans lequel nous vivons, avec ses trois dimensions spatiales et sa dimension temporelle. Il n’est pas difficile d’imaginer, et beaucoup d’auteurs de science-fiction l’ont déjà fait, que des êtres intelligents puissent exister dans un espace à 4 dimensions, mais un espace à deux dimensions offre si peu de libertés que l’on a cru pendant longtemps que des organismes à 2 dimensions ne pouvaient pas exister. » Il est amusant de spéculer sur une physique bidimensionnelle et sur les types de montage mécaniques simples réalisables dans un monde plan. »
Cela est difficile à croire mais A.Dewdney (un informaticien de l’Ontario) a réellement posé les fondements de ce qu’il appelle un planivers, c’est à dire un monde plan, à deux dimensions, et complet avec ses propres lois chimiques,physiques, astronomiques et biologiques;le planivers est pratiquement analogue à notre propre univers et apparemment dépourvu de contradictions internes. » Il … Pour éviter que son projet baroque ne dégénère en une spéculation futile, A.Dewdney adopte deux principes fondamentaux. Le principe de similitude énonce que le planivers doit ressembler autant que possible à notre univers:un mouvement sans influence extérieure doit être rectiligne, l’analogue plan d’une sphère est un cercle, etc. Le principe de changement postule que dans le cas où l’on est contraint de choisir entre deux hypothèses contradictoires-chacune également valable dans notre univers-, la plus fondamentale des deux doit être choisie et l’autre modifiée. Pour déterminer quelle est l’hypothèse la plus fondamentale, A.Dewdney s’appuie sur la hiérarchie suivante:la physique est plus fondamentale que la chimie, la chimie est plus fondamentale que la biologie etc. » Et voilà, ce n’est pas plus difficile que cela de créer un univers… En réalité, l’article dont je vous parle est long de sept pages dûment illustrées. C’est là que vous intervenez, ami lecteur féru de maths, de physique, de chimie, de biologie, d’astronomie, de stratégie des jeux, de circulation routière, de poésie, de philosophie et autres sciences exactes ou moins exactes. Votre rôle consiste à me faire parvenir pour les prochains numéros de cet opuscule vos découvertes, théories fumeuses, ainsi que vos critiques les plus vives du genre de: »Goulu, ton truc ça ne colle pas parce que… ». Ne rêvez vous pas de réinventer la poudre, de redécouvrir la relativité restreinte, la gravitation universelle. Vos noms seront élevés dans cet établissement à un rang proche de ceux d’Einstein, Newton, Beaudelaire ou Chevallaz … Quelques tuyaux:le planivers étant composé d’atomes eux mêmes composés d’électrons vibrant autour de protons et de neutrons, les couches électroniques étant ramenées à un espace plan*- les éléments chimiques peuvent-ils exister? Sont-ce les mêmes que ceux de Mendeleieff? Comment les baptiser en relation avec les éléments tridimentionnels? La cristallographie est-elle une science planiverselle? Voilà pour la chimie. Et en physique, que devient la gravité(easy)? Et la résistance des matériaux(hic)?
Comment fonctionne une grue, une machine à vapeur, une serrure? Pour les esprits moins scientifiques, peut-on jouer aux échecs planiversels( en enlevant une dimension, cela revient aux échecs linéaires), au go, aux dames, au jass? Pour les linguistes, quels mots de la langue française n’existent pas au planivers? Lesquels ont un sens au planivers et n’en ont pas ici? La feuille de papier ne pouvant exister, de quels moyens disposent les habitants pour immortaliser leurs connaissances et leurs oeuvreslittéraires? Quels sont les arts planiversaux et quelles sont leurs particularités? Pour les sportifs, quels sports, jeux et autres occupations de culture corporelle peuvent exister en, planivers? Découvrez leurs règles du jeu. Pour les autres(s’il en reste), quel est le code de la route planiversel? Comment nommer les habitants, les animaux, les lieux géographiques? Ce texte ne peut pas ne pas vous inspirer. L’Amérique est déjà découverte et lc lune est trop éloignée. Le planivers se cache dans votre tête, il suffit d’aller le chercher… Ce premier divertissement, basé essentiellement sur la spéculation et le rêve comporte des parties pour tous les intérêts, pour tous les esprits et de toutes difficultés. Des prix récompenseront les meilleures découvertes: il sera décerné en effet des prix LEBON de physique, de chimie, de médecine-biologie, de sociologie, de littérature plus un prix spécial récompensant l’oeuvre la plus humoristique, chacun de ces prix consistant en un franc suisse symbolique. A vos cerveaux…
Intéressant article sur ce sujet à http://www.askamathematician.com/2012/05/q-what-would-life-be-like-in-higher-dimensions/ , qui relève que même la lumière ne peut pas exister dans un espace à plus ou moins de 3 dimensions, car le champ électrique ne peut y être perpendiculaire au champ magnétique…
Et quid des dimensions non-entières avec lesquelles ont caractérise les objets fractales ? Ont-elles une signification physique ou sont-elles seulement une notation pratique et imagée nous permettant de les étudier ?
Peut-on imaginer un univers fractal de dimension spatial égal à 2,7 par exemple ?
Merci à Owni Science au passage de m’avoir fait découvrir ce blog qui a l’air passionnant!
Merci également à Owni Sciences de m’amener de nouveaux lecteurs avec des questions intéressantes 🙂
Pour autant que je le sache, la notion de dimension fractale est mathématique plutôt que physique. Par exemple des courbes (normalement de dimension 1) fractales tracées sur un plan (de dimension 2) ont des dimensions fractales comprises entre 1 et 2, et des surfaces fractales dans un espace 3D ont des dimensions comprises entre 2 et 3.
L’article de la Wikipédia sur le sujet me semble très bien si vous voulez en savoir plus, et il y a aussi une impressionnante liste de fractales avec leur dimension (qui m’inspirent au moins autant d’articles futurs )
Personnellement je n’arrive pas à imaginer une dimension fractale « physique » sans lien avec des dimensions entières, mais qui sait ? Certains calculent la dimension de Hausdorff de cordes quantiques (et aboutissent à un entier =3 …) , et ce cher Minkowski donne son nom aussi à une mesure de dimension fractale, ce qui tendrait à indiquer que la porte de la recherche n’est pas fermée de ce côté là.
A mon humble avis il y a encore un autre « petit détail » à éclaircir sur les dimensions spatiales et temporelles c’est de savoir si elles sont continues ou quantifiées (par les « longueur de Planck » et « temps de Planck » ?), comme dans le Jeu de la Vie. Dans la longue « liste des articles à faire », il y en a un sur le livre « Au pays des Paradoxes » de Jean-Paul Delahaye où il montre que la réponse au bon vieux paradoxe de Zénon dépend du « petit détail »…
l’article a été repris par OWNI Sciences
Votre article est vraiment stimulant. Mais je suis d’accord avec quentin et Ekho : nous ne connaissons que notre univers, le reste n’est qu’extrapolation. Xochipilli pose une excellente question : «pourquoi à 4 dimensions spatiales les forces ne décroissent-elles pas comme le carré de la distance?». J’aimerais nuancer la réponse de Jean. Au fond, la question est de savoir ce qu’il convient d’extrapoler de notre univers à un univers à 4 dimensions spatiales. Est-ce que Dieu aurait pu créer un univers à 4 dimensions spatiales ou la force de la gravitation varie comme l’inverse du carré des distances ? Vraisemblablement, mais pour cela il devrait compliquer la façon dont la force gravitationnelle s’exerce.
Lors qu’une masse B subit une force gravitationnelle due à une masse A, il faut bien qu’elle soit informée d’une façon ou d’une autre de la présence de cette autre masse. Imaginons qu’une masse A envoie constamment des messagers dans toutes les directions qui vont tout droit et tous à la même vitesse. Lorsqu’une autre masse B reçoit un messager, elle se dit : «je dois respecter la loi de la gravitation et me dévier un peu ma trajectoire dans cette direction». Remarquez que le messager n’a pas besoin de savoir à quelle distance se trouve la masse A : il suffit que la masse B réagisse de la même façon chaque fois qu’elle reçoit un messager. En effet, Plus la masse B est éloignée de A, plus les messagers seront parsemés, et moins B recevra d’impulsions pour dévier sa trajectoire en direction de A.
Il est facile de voir que dans notre univers cette force décroit avec le carré de la distance. Imaginez deux sphères centrées en A, la première est d’un rayon 1 et la seconde d’un rayon 10. Comme tous les messagers vont à la même vitesse, ceux qui sont sur la sphère de rayon 10 à un moment donné sont les mêmes qui étaient sur la sphère de rayon 1 un certain temps avant. Donc la quantité de messagers est la même sur les deux sphères (je suppose que A est immobile, plus exactement je m’assieds sur A). Mais la surface de la sphère de rayon 10 est 100 fois plus grande que celle de rayon 1. La densité de messagers, et la force sur B, y est donc 100 fois plus petites. Si on fait le même raisonnement dans un univers à quatre dimension spatiale, alors les sphères sont remplacées par des hypersphères, et la densité des messagers (et donc la force) varie inversement au cube de la distance.
Bref, dans un univers à quatre dimensions spatiales Dieu peut vraisemblablement aussi choisir une force de la gravitation qui dépende du carré de la distance, mais il devrait alors munir les messagers d’un compteur kilométrique (pour corriger le fait que sinon la force dépendra du cube de la distance). Et cela, ça m’étonnerait qu’il veuille le faire. Ce n’est pas qu’il soit flemmard, mais si on peut en juger par notre univers, cela ne correspondrait pas à son sens de l’esthétique tout empreint de simplicité.
Ce que vous décrivez de manière très intuitive avec vos messagers revient aux formules de jean, et c’est une conséquence de la « théorie des champs ». Elle a commencé au XIXème lorsque Maxwell s’est demandé comment les ondes électromagnétiques se propageaient dans le vide, et cette approche s’est poursuivie pour la gravitation avec Einstein . En fait, les charges électriques et les masses « déforment l’espace » (voir une illustration animée ici http://www.openprocessing.org/visuals/?visualID=9151 ) et les corps vont « tout droit dans des champs courbes ». Mais il demeure que c’est une des bases de la physique actuelle et que c’est facilement généralisable à un espace à N dimensions, ce qui est justement fait dans cette étude.
La force de la théorie des champs, c’est justement qu’elle est simple : Dieu n’a justement rien à faire de spécial pour que la gravité décroisse avec le carré des distances. Or comme vous le notez, la simplicité est justement un principe (pour ne pas dire un axiome) de la science, au moins depuis Ockham et Galilée : une explication simple s’est (presque) toujours révélée meilleure qu’une compliquée.
Le Dieu de la Science actuelle est très paresseux : il a au mieux lâché un pet de quelques lois et de constantes universelles soigneusement ajustées et tout a suivi. D’ailleurs la Bible ne dit pas fondamentalement le contraire : le 7ème jour Il s’est reposé, au lieu de fignoler les détails 🙂 (c’est un gag du Chat de Geluck)
En dérivant un peu du coté scientifique de cet article et en regardant du coté de la science-fiction, j’avais écrit un article sur une hypothèse à 3D + 2T pour expliquer le déroulement de la série TV Lost il y a de cela un an je pense : http://seriestv.blog.lemonde.fr/2010/01/27/lost-week-paradoxes-des-voyages-dans-le-temps/ ma théorie m’avait pas l’air si ultra-hyperbolique que ça à l’époque 🙂
Après une bonne semaine à ruminer sur le sujet agrémenté de vos commentaires et questions, je tente une réponse collective…
D’abord, il me semble nettement plus facile d’imaginer des dimensions supplémentaires d’espace que des temps à 2D ou plus. Commençons par les dimensions spatiales.
@quentin et @Ekho je réponds comme Albert: « Ce qui m’intéresse vraiment c’est de savoir si Dieu avait un quelconque choix en créant le monde. » . Cette étude comme celles sur les constantes universelles vont plutôt en direction de « Non, Il n’avait pas le choix ». Cette étude sur les dimensions ne me semble pas du tout anthropique, tout au plus « biopique » dans la mesure où on recherche les conditions permettant l’émergence d’une complexité de type biologique. Et les points de départ sont simplement les fondements de la physique actuelle : les champs et le « modèle standard », et on montre que 3D+1T est le seul « choix » permettant à la fois aux particules de former des structures complexes en certains rares points (les planètes) où les conditions physiques restent constantes pendant « longtemps » grâce aux orbites stables. Difficile d’imaginer moins « anthropique » me semble-t-il.
Merci @jean d’avoir répondu @Xochipilli. (faut que j’installe un plugin LaTeX…). C’est ça aussi pour l’énergie d’une onde lumineuse ou autre qui se disperse sur la surface (de dimension N-1) d’une sphère centrée sur un émetteur à N dimensions.
@Nicobola : Difficile aussi d’imaginer quelque chose d’encore plus fondamentalement différent de la physique que nous connaissons. A ce titre je trouve que les automates cellulaires type « jeu de la vie » à 2D+1T sont un bon point de départ. Reste à imaginer une physique qui permette l’émergence et la « vie » de telles structures, en particulier la circulation de l’énergie…
@Gaurbhack et @Yves : les dimensions temporelles c’est beaucoup plus dur à imaginer, entre autres parce qu’on a pas une idée claire de la nature physique du temps. Dans les études citées on dit à la fois que le temps est la dimension dans laquelle nous ne maîtrisons pas nos déplacements (nous sommes forcés de la parcourir à une vitesse de 1 seconde par seconde… ), et du point de vue mathématique c’est assez simple, c’est une dimension dans la direction « imaginaire » : dans la métrique de Minkowski qui « relativise » Pythagore en 3D, le carré d’une distance temporelle apparaît avec un signe opposé aux carrés des distances spatiales.
Dans l’article de Tegmark, les dimensions temporelles supplémentaires conservent ces deux attributs : imaginaires (donc on reste dans un espace « simplement complexe » et non hypercomplexe par exemple (faudra que j’écrive sur les hypercomplexes, parce que c’est beau ) et « incontrolable », donc qu’on ne peut pas se déplacer dans le temps comme on veut, mais qu’on « subit » son écoulement…
Mais comme le relève Goldberg, ça implique que les dimensions temporelles soient indépendantes, car si le temps s’écoulait de façon corrélée dans deux dimensions, on ne percevrait que son « écoulement » le long de la ligne d’intersection entre les deux espaces 3D+1T et 3D+1T’, un peu comme ce que suggère Gaurbhack.
J’ai essayé de me représenter ceci dans l’univers 1D+2T, qualifié de « too simple » par Tegmark en imaginant un univers linéaire comme une voie ferroviaire, peuplé par des locomotives. La position d’une locomotive sur le rail est une fonction x(t1,t2) des deux temps, mais elle s’y déplace à « deux vitesses » v1=dx/dt1 et v2=dx/dt2, ce qui permet aux locomotives de se dépasser ou de se croiser sur le rail facilement en actionnant au hasard leurs moteur v1 et v2 : il n’y a qu’une chance infime pour que la distance entre 2 locomotives d2=(x-x’)2-(t1-t1′)2-(t2-t2′)2 provoque une collision. Au point où, comme le note Tegmark, la difficulté est plutôt de rencontrer « volontairement » une autre loco car une loco située en (x,t1,t2) ne peut voir que les autres locos qui « traversent » l’instant (t1,t2) comme des éclairs juste devant ou juste derrière le point x. Comment mesurer instantanément les deux vitesses de l’autre loco pour les rattraper ? comment leur transmettre un point de rendez-vous ? Comment assurer la reproduction des locomotives ? 😉
1D+2T est un univers très simple, mais déjà très déroutant car les informations que l’on peut tirer de l’environnement sont très largement insuffisantes pour s’en faire une image assez complète pour permettre un minimum de prédiction.
@Gaurbhack : L’idée de dimension « cachée » traduisant l’aspect fondamentalement aléatoire de la mécanique quantique me plait assez (bonjours les univers parallèles), mais je ne suis pas sur que ça entre dans une métrique à la Minkowski. Il faudrait pouvoir quantifier la « distance » entre deux évènements co-localisés et simultanés qui ne se distingueraient que par un choix aléatoire… Comment combiner un « pile ou face » avec des mètres et des secondes., that is the question.
Vraiment intéressant
Est ce qu’il se pourrait qu’on soit dans un univers avec un temps de plus d’une dimension, mais sans qu’on en ai conscience? Le premier axe des temps représente le temps que l’on connait, les autres partie représente les « choix », la physique quantique peine à être déterministe, ça serait une solution élégante, à chaque indétermination, plusieurs univers émergent… 🙂
@Xochipilli
Il est assez naturel de supposer que le potentiel $latex phi $ du champ de gravitation vérifie l’équation:
$latex Laplacien(phi)=rho $
avec rho la densité de masse.
Si on prend $latex rho=delta $ (masse ponctuelle en zéro), alors:
$latex phi=C/r^{N-2} $
(Cela se démontre avec une formule de Gauss appliquée au champ gravitationnel sur une hypersphère de rayon r. C’est l'(hyper)-aire [proportionnelle à $latex r^{N-1} $] de l’hypersphère qui donne la décroissance en $latex 1/r^{N-2} $ du potentiel de gravitation)
Wouah! C’est fascinant, mais j’ai pas tout compris: pourquoi à 4 dimensions spatiales les forces ne décroissent-elles pas comme le carré de la distance?
Intéressantes réflexions! Auxquelles je me permet de soumettre ces remarques. « Prédiction »: elles sont faites par un cerveau noyé dans la 3D+T, mais un cerveau équipé dans un univers 3D+2T n’en aurait-il pas intrinsèquement la capacité? La 2T en ferait partie intégrante.
Quand à notre univers 3D+T, il souffre d’une distorsion entre le temps et les dimensions, mise en évidence par Albert: si les objets 3D sont déplacé rapidement, il changent de taille. Ou si une horloge est déplacée rapidement, elle change de temps.
Je suis loin d’avoir chopé toutes les subtilités mais ces questions de vie dans d’autres univers me laissent dubitatif. Si on suppose la vie terrestre évidemment que ce n’est pas possible dans d’autres univers mais sur d’autres planètes non plus ^^ Si on élargi le concept de vie pourquoi ne pas imaginer des systèmes vivants selon ce concept dans des univers qui suivent des règles différentes? Par exemple il est supposé ici que la vie existerait sur une planète, ce qui est déjà centré sur la vie terrestre ou du moins dans notre univers! Bref, c’est un article interessant ^^
Je suis assez d’accord avec Quentin… L’article est très intéressant, mais se base exclusivement sur notre espace-temps à 3+1 dimensions (d’ailleurs, comment pourrait-il en être autrement).
L’ajout d’une dimension (spatiale ou temporelle) est une modification tellement fondamentale de notre « univers habituel » qu’y étendre nos « lois habituelles » me semble un brin présomptueux.
Ceci étant, je maintiens, article très interessant.
L’argument anthropique est un peu frustrant.
En gros, on n’explique pas pourquoi il y a 3+1 dimensions, mais pourquoi il ne pourrait pas en être autrement, ce qui est légèrement différent. Est-ce que ça veut dire que, comme par hasard, l’univers (ou Dieu, ou je ne sais quoi) a choisit pile-poile les bonnes valeurs pour qu’on puisse exister, et faut-il en conclure qu’on a vraiment de la chance d’exister ? C’est le genre d’arguments susceptibles de beaucoup plaire aux créationnistes… (ça ne peut pas être le hasard, donc c’est Dieu). Ou bien est-ce que toutes sortes d’univers existent, mais que seuls ceux qui ont le bon nombre de dimensions donnent lieu à des êtres vivants ?
Question subsidiaire : puisqu’on en est à imaginer toutes sortes d’univers possible, au nom de quoi doit-on partir du principe que dans ces autres univers, les forces décroissent de la même façon avec la distance, ou que les critères de stabilités sont les mêmes ? En gros, pourquoi ces principes seraient plus sûrs et plus absolus que le principe suivant lequel il existe trois dimensions spatiales et une de temps ?