La fraternité des nombres

Vu l’autre jour sur un blog¹ une « question bête », donc intrigante : existe-t-il des nombres entre lesquels les mathématiciens ne connaissent aucune relation ?

La question est « bête » puisqu’on peut toujours trouver une relation entre deux nombres entiers. Mais elle m’a rappelé ma quête initiée avec les nombres acratopèges : tous les nombres ont de nombreuses propriétés répertoriées en particulier dans l’ Encyclopédie en ligne des suites de nombres entiers de Sloane, mais certains en ont nettement plus que d’autres.

En utilisant la même approche (la base de données de Sloane digérée par quelques lignes de Python), j’ai établi le lien de « fraternité » entre les entiers de 1 à 1024, en comptant pour chaque paire (a.b) possible  le nombre de suites comportant ces deux nombres, que j’appelle la fraternité f(a,b).

Par exemple, 456 et 789 ont une fraternité f(456,789) = 32, car ils sont présents dans 32 séries et partagent donc autant de propriétés répertoriées.

Les nombres les plus fraternels sont évidemment 1 et 2, qui sont présents dans 133529 séries répertoriées à ce jour. A l’inverse, les deux plus petits entiers qui ne partagent aucune propriété sont 48 et 857².

52 et 991 sont les plus petits nombres ayant une seule propriété commune, en l’occurence celle-ci

J’ai représenté les fraternités  f(a,b) pour a et b variant de 1 à 1024 dans l’image ci-dessous. Le point (1,1) est en bas à gauche. Les fraternités f(a,b)>100 sont représentées par des pixels rouges et les fraternités inférieures à 10 sont en bleu foncé. Les quelques pixels noirs dénotent les fraternités f(a,b)=0.

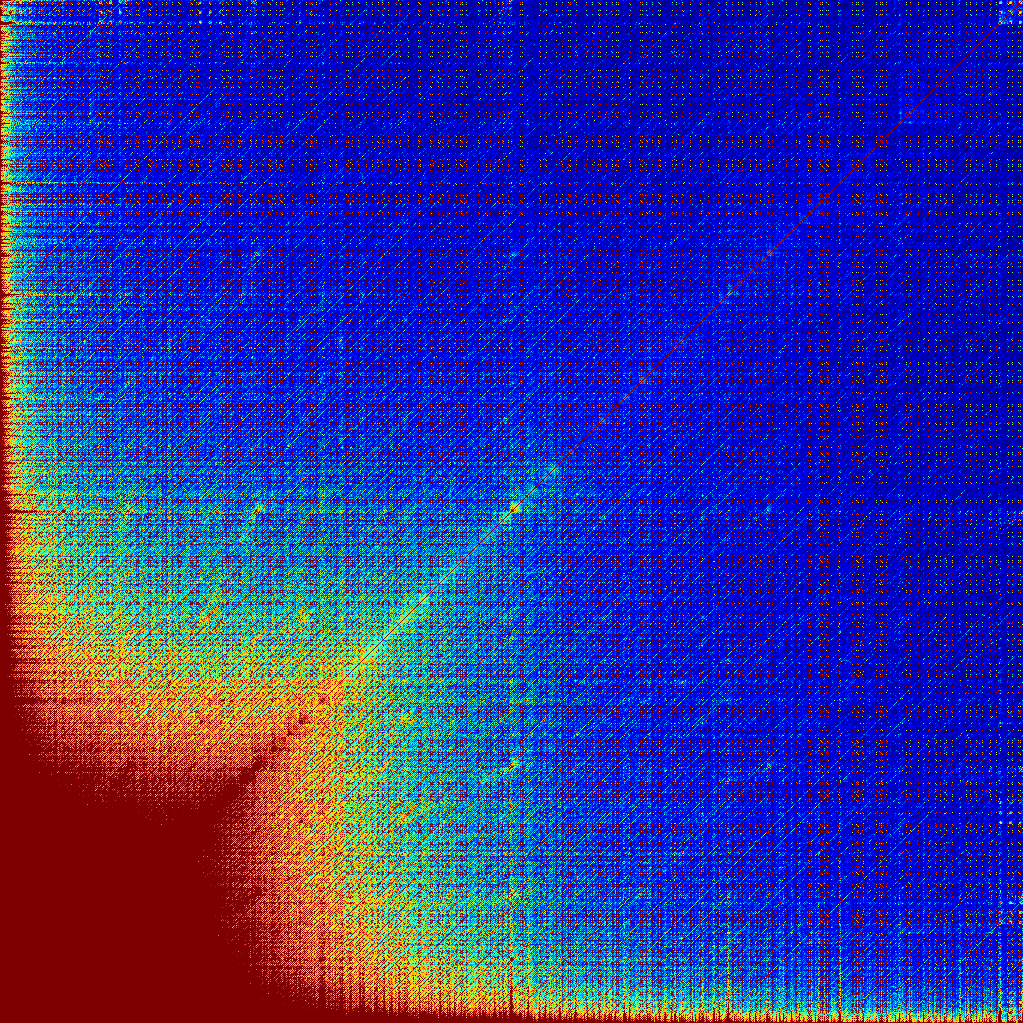
On remarque l’apparition de quelques motifs:

• les lignes horizontales et verticales claires correspondent à des nombres particulièrement minéralisés, les sombres aux acratopèges
• les lignes claires à 45° sont plus surprenantes. Elles semblent indiquer que des nombres consécutifs ont tendance à être plus proches d’autres nombres consécutifs séparés par des constantes. Je m’attendais à voir apparaître des lignes à 30° et 60° liant les nombres à leurs doubles, mais ce n’est pas le cas.
• Sur la diagonale (coloriée en rouge par convention), on distingue des petites taches autour de groupes de nombres particulièrement intéressants comme les fortement composites (160, 320) et les puissance de 2 (256, 512), qui forment aussi des taches aux intersections hors diagonale.
• Les motifs les plus étranges sont les groupes de 9 points clairs visibles le long des bords bleus, et en particulier au coin supérieur droit. Ils correspondent aux nombres 1010±10 et 110±10, ce qui peut s’expliquer par les nombreuses suites faisant intervenir des nombres binaires, mais on en trouve aussi à 210±10. Est-ce l’effet du ternaire, ou d’autre chose ?

Résultat provisoire de ma recherche aussi excitante qu’inutile : les nombres ne sont décidément  pas tous égaux devant les mathématiques.

Notes:

1. je ne retrouve plus la source de la « question bête ». Elle a été posée il y a une semaine sur un blog… Si vous savez où, merci de me l’indiquer en commentaire…
2. Le moteur de recherche de l’Encyclopédie de Sloane peut soit trouver des termes consécutifs dans la série, soit des nombres présents dans tout l’article dédié à chaque suite. C’est pourquoi la recherche de 48 et 857 fournit plusieurs résultats, mais si vous regardez bien, les nombres 48 et 857 ne sont jamais présents ensemble dans les séries.