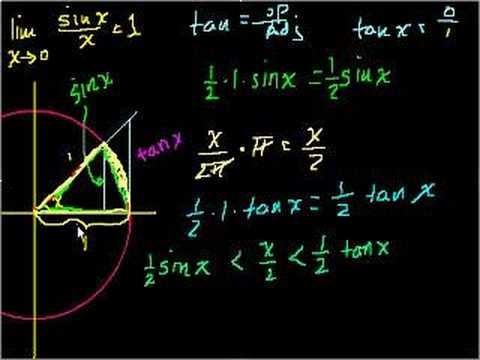La bonne manière de calculer des trucs

“The Right Way to Calculate Stuff”  est une page pour informaticiens dans mon genre : elle contient des petits “snippets” de code utile pour contourner certains pièges tendus par les maths et la géométrie.

Par exemple, si on veut calculer sin(x)/x, il faut faire attention à ce qui se passe pour x=0, sinon on obtiendra une erreur de “division by zero” au lieu du résultat attendu, qui est 1. Un bon programmeur prévoira le coup en écrivant (en C++) :

if (x == 0.) return 1. else return sin(x)/x;

mais ce n’est peut-être pas suffisant. Si x est très petit, la division de deux nombres très petits approximés par nos chers ordinateurs a des chances d’être assez fausse. Pour des raisons expliquées en détail sur la page, il faut s’assurer en fait que x2 est encore un nombre numériquement assez grand par rapport à 1, donc un très bon programmeur écrira ceci :

if (1. + x*x == 1.) return 1. else return sin(x)/x;

ce qui parait mathématiquement absurde puisqu’on imagine pas que 1+x2 puisse valoir 1 pour x≠0. Mais informatiquement, c’est très possible.

L’article donne ainsi une série de recettes pour calculer des expressions dangereuses, par exemple :

• 1-cos(x) → 2*sin(x/2)2
• acos(1-x) → 2*asin(sqrt(x/2))
• et bien d’autres

Mais les recettes les plus intéressantes (en tout cas pour moi) concernent la géométrie.

Pour calculer l’angle entre 2 vecteurs u et v, l’ “approche pachyderme” comme disait Burgi consiste à évaluer acos(dot(u,v)), dot étant la fonction renvoyant le produit scalaire des 2 vecteurs. mais si u ou v ne sont pas parfaitement normalisés et que dot renvoie un résultat un pouillème plus grand que 1 : crash.

une deuxième approche est: 2*atan2(abs(u-v),abs(u+v)). Pas mal mais couteux en temps de calcul. La meilleure implémentation est

if (dot(u,v) < 0.)
  return M_PI - 2*asin(abs(-v-u)/2)
else
  return 2*asin(abs(v,u)/2);

La partie vraiment intéressante concerne l’interpolation sphérique linéaire . (Comme c’est assez spécifique à la 3D, je publie aussi ce qui suit sur mon blog 3Dmon  )

L’orientation d’un corps dans l’espace à 3 dimension est défini par 3 angles tout comme la position d’un objet posé sur une sphère est définie par les 2 angles de latitude et de longitude, plus un angle définissant l’orientation de l’objet

Le problème consistant à faire tourner “en douceur” un objet dans l’espace pour l’amener dans une orientation déterminée est appelé “interpolation sphérique linéaire” parce qu’il est équivalent à celui consistant à se déplacer “en douceur” sur une sphère pour atteindre une position et une orientation donnée. Le problème n’est pas trivial pour 2 raisons:

1. comme les angles sont définis “modulo 360°”, il faut que l’interpolation en tienne compte : si on va par exemple de la longitude -179° à la longitude +179°, il faut faire 2° dans le sens négatif et pas 358° dans le sens positif.
2. quelle que soit la manière dont on définit les 3 angles, il existe des “singularités” aux point analogues aux pôles : à la lattitude 90°, la longitude n’a plus d’importance mais si on passe par le pôle, il faut “se rappeler” de notre dernière longitude pour pouvoir continuer “tout droit” dans la longitude augmentée de 180° (modulo 360°), et simultanément éviter qu’une mauvaise description de l’angle d’orientation nous fasse faire brusquement un demi-tout sur nous mêmes en passant par le pôle pour conserver un angle par rapport au nord …

“The right way to calculate stuff ” décrit la fonction “slerp” [1] qui définit l’interpolation sphérique linéaire entre 2 vecteurs unitaires $v_0$, $v_1$ ainsi:

où $a$ est l’angle entre $v_0$ et $v_1$ calculé comme indiqué plus haut. Mais il est clair que pour des angles tels que $\sin(a)$ est nul ou très petit, des problèmes numériques vont survenir. En travaillant un peu la fonction slerp peut s’écrire:

où sin_over_x est la fonction $\sin(x)/x$ calculée de façon robuste, toujours comme indiqué plus haut

Reste à traiter le cas ou a est proche de 180°, ce qui revient à retourner un objet, ou à aller aux antipodes du point où on se trouve sur le globe. Il y a alors une infinité de trajets possibles, et il faut bien en choisir un plutôt que de laisser l’ordinateur se planter…

Références:

1. Ken Shoemake, Animating rotation with quaternion curves, SIGGraph ‘85 proceeding