Après une petite pause due en partie au déménagement de ce blog suite à des problèmes d’hébergement, je vous propose une traduction de l’article « Falling faster than gravity » de Sedeer sur Inspiring Science. Pour la petite histoire, ça me rappelle une question que je m’étais posé une nuit d’insomnie à bord d’ « Etoile Filante » : ma couchette pouvait-elle vraiment tomber plus vite que moi lorsque le bateau franchissait une vague ?
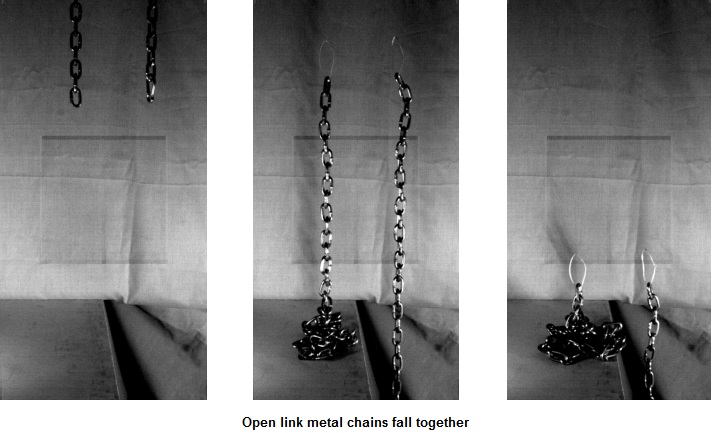
En 2011, une équipe de physiciens de l’Université Cornell à Ithaca (New York) a montré que lorsqu’une chaîne en chute libre heurtait quelque chose, par exemple une table, elle pouvait, contrairement à l’intuition, accélérer et tomber plus vite que si elle ne touchait rien. En étudiant attentivement sa mécanique, ils ont montré que l’impact pouvait tirer le reste de la chaîne vers le bas. Comme le montre la photo de leur expérience ci-contre, ils avaient raison. Les deux chaines bizarres ont été lâchées de la même hauteur au même moment, mais celle de gauche qui tombe sur une table en formant une pile est tombée plus vite que celle de droite qui tombe à côté de la table.
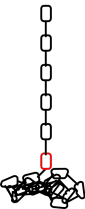Anoop Grewal, Phillip Johnson et Andy Ruina ont découvert ceci en réexaminant un problème classique des cours de physique : la chaîne qui tombe sur une pile. La solution standard part du principe que le maillon qui heurte la table (en rouge sur le dessin) se déconnecte du maillon supérieur au moment de l’impact, donc qu’il s’arrête sans influencer le reste de la chaîne. C’est une hypothèse raisonnable étant donné que les maillons d’une chaîne sont assemblés de manière très lâche, mais l’équipe n’était pas convaincue que ce soit toujours le cas. Si le dernier maillon continuait à interagir avec le maillon du dessus, il pourrait exercer une force sur la portion de la chaîne encore en train de tomber. Suivant la direction de cette force, l’impact des maillons pourrait ralentir, mais peut-être aussi accélérer la chute du reste de la chaîne.
Comment un tel mécanisme pourrait-il réellement fonctionner en pratique ? L’équipe est parvenue à concevoir plusieurs types de chaînes où l’impact des maillon peut tirer sur le reste de la chaîne. Le plus simple est basé sur l’idée d’un barreau tombant au sol. Si le barreau est incliné, une de ses extrémités touche le sol en premier, et l’autre extrémité pivote autour du point de contact avec le sol, ce qui la fait tomber plus vite. L’extrémité libre accélère pour la même raison que vous vous mettez à tourner rapidement si vous saisissez un point fixe en courant ou en patinant : c’est la conservation du moment angulaire.
Tout ce qui est attaché à l’extrémité libre, par exemple par une ficelle, sera tiré vers le bas. Ainsi, l’impact du barreau avec une surface crée une force qui tire le reste de la chaîne. C’est contre-intuitif, et ça peut même paraître fou, mais c’est vrai. Le trio a construit des chaînes selon ce concept, elles ressemblent à des échelles de corde de traviole, et les a utilisé une caméra video à haute vitesse pour en filmer une paire tombant côte-à-côte. Comme ils l’avaient prévu, la chaîne tombée sur la table est tombée plus vite que celle tombant à côté : (video : Ruina Lab):
Ils ont aussi testé une chaîne ordinaire, qui se comporte juste comme on s’y attend. Dans ce cas, le dernier lien se déconnecte du précédent et ne lui applique donc aucune force, ce qui signifie que l’hypothèse utilisée pour résoudre le cas d’école est valide dans ce cas.
Alors qu’on peut mesurer et comprendre les fluctuations de l’univers primitif, il est quand même étonnant que l’on puisse encore apprendre de nouvelles choses sur quelque chose d’aussi familier qu’une chaîne tombant au sol. Je finis souvent mes articles en m’émerveillant sur l’immense richesse du monde, mais cette fois c’est notre capacité à toujours nous poser des questions et à comprendre le monde avec précision qui m’étonne.
La science qui nous permet de construire des ponts et des avions, d’envoyer des sondes au delà de notre système solaire et d’explorer les vallées océaniques est la même que cette science a permis à ces chercheurs de prévoir et de confirmer un résultat si étrange, si contre-intuitif à propos de quelque chose d’apparence si commune. Les petits mystères et les merveilles quotidiennes abondent. Ils n’attendent que d’être découverts et décrits par un esprit curieux, et c’est ce qui rend la science si fantastique!
Référence
- [altmetric doi= »10.1119/1.3583481″ float= »right »]Grewal, A., Johnson, P., & Ruina, A. « A chain that speeds up, rather than slows, due to collisions: How compression can cause tension » 2011, American Journal of Physics, 79 (7) DOI: 10.1119/1.3583481
16 commentaires sur “Comment tomber plus vite que la gravité”
Imposible.Revoir les decouvertes du plus grand genie de ce millenaire alias Isaac Newton
Très juste : revoyez Newton et appliquez ses lois à une barre qui tombe inclinée au sol. Son énergie cinétique e=0.5*m*v^2 (1) se transforme en énergie de rotation e=0.33*m*l^2*w^2 (2) ou w^2 est la vitesse de rotation de la barre autour de l’extrémité qui heurte le sol, ce qui donne une vitesse v’=w.l de l’autre extrémité. En égalant les deux équations (1 et 2), on obtient v’=sqrt(1.5).v , donc la vitesse de l’extrémité est 22.5% plus élevée que la vitesse de chute, ce qui tend le fil avec une force f qui accélère le reste de la chaine de masse M selon f=M.a pendant un petit temps t. Pendant ce temps, la barre décélère jusqu’à ce que son extrémité tombe à la même vitesse que la chaîne qui a été un peu accélérée vers le bas (calculs dans l’article).
Bref c’est surprenant, mais pas impossible du tout, même Newton serait d’accord.
Une simple simulation, avec WorkingModel par exemple, montre très bien l’effet
Si on regarde l’échelle de corde en entier (donc en incluant la partie déjà au sol), son centre de gravité ne tombe pas plus vite que la gravité.
Même si effectivement le mouvement du haut de l’objet peut surprendre au premier abord, ça n’apporte rien à ce qu’on connaît déja de la mécanique.
Effectivement, c’est comme l’oeuf de Colomb : une fois qu’on voit le truc, c’est évident. Et on cherche toujours une application…
un collègue fan de site conspirationniste m’avait dit que lors de l’attentat du world trade center, les tours jumelles s’étaient éffondrées plus vite que la chute d’un objet normal. Je n’ai pas vérifié le sujet mais ça m’avait marqué comme argument. Peut-être que la structure de la tour a réagi comme l’échelle de corde en tirant vers le bas l’ensemble de l’édifice. Bon tout cela n’est pas vérifié en tout cas l’article est fort intéressant. Merci
d’après cette vidéo http://www.youtube.com/watch?feature=player_embedded&v=qLShZOvxVe4 et les analyses sur http://www.debunking911.com/freefall.htm les tours sont tombées plus lentement que les 9.2 secondes de chute libre. Dans « conspiration », il y a « piration »…
Oui!!!
Encore plus enigmatique que le mode de fonctionnement des femmes…..C’est pour dire!
surprenant en effet !
Un grand MERCI à vous DR goulu.
Comprenez vous mieux maintenant en quoi un esprit particulier peut se poser des questions particulières et trouver comment tirer partie des réponses trouvées?
Comment configurer une « situation » pour qu’elle produise plus que son original classique et en extrapolant comme je l’ai fait:comment passer de zéro à quelque chose….
C’est simplement la preuve qu’une infime subtilité technique peut tout changer.
Ca montre surtout qu’une bonne compréhension de la physique est indispensable pour découvrir ou inventer des systèmes qui fonctionnent 😉
Celui là est sympa, mais je le trouve beaucoup moins surprenant que le DDWFTTW par exemple.
Oui, et oui. O:-)
Un article très intéressant en effet, et qui m’a rappelé les interminables discussions avec les complotistes du 11 septembre sur la vitesse d’effondrement des Twin Towers … on voit en l’occurrence que des tas d’effets contre-intuitifs peuvent se produire et que les « on voit bien que » sont à prendre avec prudence.
Merci pour avoir relevé l’article, et pour la traduction !
Personnellement ce qui m’étonne, c’est que tu sois encore étonné de toujours t’étonner ! 😉
en fait le dernier paragraphe fait toujours partie de la traduction, et je m’y reconnais à 100%, donc je ne suis pas seul 😉
Et donc finalement tu apportes toi-même la preuve pas l’exemple qu’intuitivement(*), on peut quand même arriver à comprendre véritablement certaines choses 😉
(*) parce que mon incommensurable intelligence analytique n’était pas intervenue, sur ce coup, je m’étais juste laissé bercer par la poésie de ton âme d’enfant émerveillé. :o)