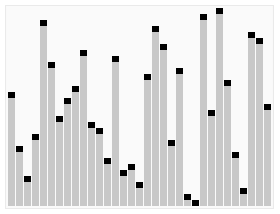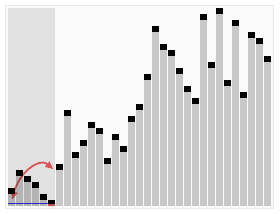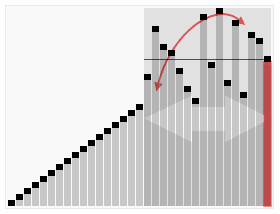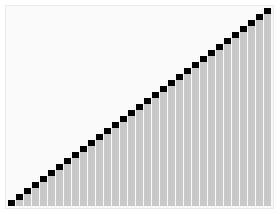
En informatique, le tri est une opération incontournable car il est beaucoup plus rapide de rechercher une information dans une liste triée que dans un fouillis. C’est pourquoi j’ai longtemps cru qu’une liste triée contenait plus d’information qu’une liste non triée, car je voyais le tri comme un pré-traitement permettant d’accélérer les opérations suivantes, donc un « plus » par rapport à une situation « moins » performante.
Pris d’un doute il y a quelques années, j’avais posé la question sur un forum consacré à l’informatique théorique :
« est-ce qu’une liste triée contient vraiment plus d’information qu’une liste non triée ?”
Un érudit professeur m’avait répondu simplement ceci :
« ce contient d’ est- information liste liste? non plus qu’ qu’ triée triée une une vraiment ».
J’ai mis un moment à comprendre la profondeur de cette réponse : ma question, une fois les mots triés par ordre alphabétique, était devenue incompréhensible, et contenait donc moins d’information que la phrase originale ! Depuis je sais que l’informatique détruit toujours l’information.
Ce petit concours a reposé la question sous un angle intéressant : est-il possible de programmer un algorithme de tri « réversible », permettant de remettre une liste triée dans son état initial ? Évidemment oui : il suffit de stocker en plus l’information perdue lors du tri, le plus simple étant de mémoriser l’état initial de la liste par exemple en ajoutant à chaque élément trié son numéro d’ordre :
« ce2 contient7 d’10 est-1 information11 liste5 liste14 non15 plus9 qu’3 qu’12 triée6 triée?16 une4 une13 vraiment8 ”.
Pour une liste contenant n éléments, on a besoin de log(n) bits* pour stocker chaque numéro, donc de n.log(n) bits au total.
Peut-on faire mieux? On pourrait se dire que beaucoup d’algorithmes de tri comme QuickSort permutent des éléments après les avoir comparés, et qu’il suffirait donc de stocker le résultat des comparaisons effectuées, soit un bit par test, pour pouvoir ensuite « défaire le tri » en parcourant la liste des bits à l’envers. Combien faut-ils de bits ? ben … au moins n.log(n) aussi puisque c’est justement le nombre de comparaisons qui détermine la « complexité » des algorithmes de tri, et que les bons algorithmes ont une complexité de n.log(n).
Rien ne sert de se casser la tête sur « algorithme de tri réversible », il ne peut pas être plus efficace que de simplement stocker l’ordre initial des données. Etonnant non ?
Le problème, c’est que la donnée du concours spécifie qu’on n’a le droit de stocker que 50% d’information supplémentaire par rapport à la taille des données : si on trie 4K octets, on n’a droit qu’à 2K de données supplémentaires. Or en fonction de ce qui précède on a besoin de 4096*log(4096) bits, soit 6K, plus que les données! En passant, ça signifie qu’en triant beaucoup de petites données, on peut perdre plus de la moitié de l’information contenu dans la liste initiale !
Bref, personne n’a gagné le petit concours parce que ce n’était tout simplement pas possible.,
Note* : en informatique, log(n) dénote évidemment le logarithme binaire ou base 2




12 commentaires sur “Tri réversible ?”
Je maintiens le « donc » pour au moins deux raisons :
1) Pour te rejoindre sur Kolmogorov, un programme capable de mettre une liste de mots dans un ordre satisfaisant ne serait-ce que syntaxiquement un langage quelconque, humain ou pas, est BEAUCOUP plus complexe que celui qui les trierait selon n’importe quel critère de comparaison du type « X vient avant Y ». Donc la complexité de Kolmogorov du programme générant la phrase est plus grande que du programme produisant la liste triée.
2) la liste triée peut être comprimée par un algorithme simple (genre Lempel Ziv, .zip) beaucoup mieux que la liste non triée. Elle contient donc moins d’information.
Je sais, ça a été aussi assez dur à admettre pour moi … 😉
Ce programme n’est pas contenu dans la phrase en question. Il n’existe pas d’algo décidant si une phrase a un sens,
hors de la donnée d’un language cible (ça se voit en
tordant un peu le théorème de Rice, par exemple).
Ca, ça reste vrai, et la conclusion de ton « donc » est juste,
mais seulement pour la raison que tu donnes en 2). Pas de rapport avec la ‘compréhensibilité’.
Nous pourrions très bien parler une langue ou seules les
phrases triées aient un sens, tu vois?
Goulu,
«ma question, une fois les mots triés par ordre alphabétique,
était devenue incompréhensible, et contenait donc moins
d’information que la phrase originale !»
Ce ‘donc’ est faux, je rejoins Éric C. sur ce point. Voir la
phrase originale comme ‘non triée’, c’est oublier un peu
vite qu’elle répond à des règles assez précises : il ne
s’agit pas du tout d’une suite quelconque de mots.
Oui, dans cet exemple, le tri a écrasé le sens initial, mais
ce n’est que le point de vue d’un humain. Le « sens »
mentionné n’est pas intrinsèque à la phrase, il nécessite la
phrase _et_, pour y associer une sémantique, un moteur assez
complexe : un francophone, en l’occurrence.
Le rapport entre information (à la Kolmogorov) et sens n’est
pas si simple.
@vpo L’informatique, c’est la technique des ordinateurs, mais c’est aussi la science de l’information. Les questions soulevées par l’article concernent l’information « pure » (c’est pourquoi je marque « informatique théorique » ce genre d’articles), donc effectivement tout ceci s’applique aussi à l’armoire d’habits, et le critère de tri n’a aucune importance.
@Yves+vpo Le fait de trier détruit l’information sur l’ordre initial, qui peut être plus importante (qualitativement et/ou quantitativement) que les données elles-mêmes. Ce que je montre dans l’article, c’est qu’il n’y a pas de moyen plus efficace pour retrouver l’ordre initial de n éléments que de le stocker dans une liste qui nécessite n.log(n) bits.
@Yves J’ai pas encore tout compris, mais l’article mentionné par kelux plus haut (http://www.di.unipi.it/~grossi/PAPERS/jfocs04.pdf ) montre que l’ordre n’est pas forcément indispensable à une recherche rapide. D’après ce que j’ai compris, leur idée est proche de celle des tables de hachage : avec un « bon » désordre et une « bonne » fonction pour s’y retrouver, il est possible de retrouver l’information plus directement que par dichotomie O(log n).
Assertion Goulutienne: le tri détruit de l’information. Ce n’est pas aussi clair, car l’information stockée dans des bits est « orientée », ou plutôt, typée. Exemple: avec 4 bits, on peut:
compter jusqu’à 15 (0..15)
Désigner 16 couleurs, du noir au blanc
représenter 10 chiffres et 4 lettres (0..9, A-F)
indiquer quelle touche d’un clavier de 4 x 4 touche est pressée
etc..
En fait , que représente le tri, en tant qu’info? Rien, mais ça accélère une recherche typée. Inutile de demander à Google pourquoi il faut des indexes. Sinon une requête prendrait un tel temps qu’elle serait vaine. L’index contient donc de l’info typée. Le tri n’ajoute pas d’info, mais je ne vois pas en quoi il la détruit. Le rangement introduit est fait selon un type prédéfini, présupposé et orienté selon le sens de ce qui est stocké dans les bits en question.
Ce que je ne comprends pas bien, c’est en quoi c’est un problème propre à l’informatique et non propre au concept de tri.
Exemple : Des vêtements sont dans une armoire.
On peut se dire que si il ne sont pas triés par type de vêtement, c’est que leur proprio est bordélique et que chercher toutes les chaussettes rouges va être plus long que si toutes les chaussettes étaient triées par couleur et dans une boite séparée des autres vêtements.
Ou bien il se peut qu’il y ait une raison à l’absence de tri. Par exemple c’est l’armoire d’un maniaque qui prépare un ensemble de fringue pour chaque jour de la semaine.
Le fait de tout ranger dans l’armoire détruira l’information placée là par le proprio des vêtements.
Donc c’est le fait de trier qui est destructeur d’information en échange d’une recherche d’élément plus rapide. En l’espèce que le tri soit fait par un ordinateur ou bien par un humain, le résultat est le même mais l’ordinateur va souvent plus vite…
Alors que dans d’autres cas comme la numérisation par exemple, on peut vraiment dire que c’est l’informatique qui détruit l’information (résolution du capteur, capacité de stockage, etc…).
@kelux . Merci pour l’article, faut que je lise ça tranquillement. Je n’arrive plus à remettre la main sur le fameux forum, j’ai déjà cherché plusieurs fois… Je me demande soudain si ce n’était pas un « newsgroup »… yesss! je l’ai retrouvé ! c’est sur comp.theory ici
@Eric C. tu peux toujours chercher. L’idée c’est que l’ordre des mots d’une phrase t’apporte de l’information : le sens de la phrase. Une fois triés, les mots de la liste n’apportent plus que de l’information sur leur ordre relatif dans un dictionnaire. Retrouver le sens de la phrase initiale est au mieux très complexe (nécessite non seulement la syntaxe, mais souvent la sémantique : « la le chat mange souris » a deux solutions, dont une plus vraisemblable que l’autre si on connait les bêtes), et au pire impossible car non univoque.
@mmm : dans ton exemple, le point le plus proche dépend de façon univoque du vecteur Y, mais aussi de ton entrée x. Tu entres un point inconnu (x), la machine te renvoie un autre point (xy) extrait d’une liste connue : l’algorithme fait « entonnoir », et n’est pas plus réversible que celui du tri : Pas moyen de retrouver x à partir de xy! Une solution serait de stocker les points x entrés dans une deuxième liste X : en entrant xy, il chercherait le point le plus proche dans X. Bref, en fin de compte l’information qui parait « créée n’est jamais supérieure à celle que tu as entré dans la machine (y compris le programme) et qu’elle a stocké en attendant d’en ressortir un extrait.
Me fait penser à ce joli petit programme de 133 caractères qui génère 15000 décimales de pi : génère-t-il de l’information, ou est-elle déjé comprimée dans le programme ?
Je ne remarque que maintenant que sur la thread de comp.theory, on m’avait conseillé de regarder la transformée de Burrows Wheeler, sur laquelle je suis tombé en planchant sur ce concours de tri réversible. Peut-être le sujet d’un prochain article…
« ma question, une fois les mots triés par ordre alphabétique, était devenue incompréhensible, et contenait donc moins d’information que la phrase originale ! »
Mmoui, je trouve le « donc » un peu rapide.
En même temps, je cherche un contre-exemple 🙂
À l’inverse, en désordonnant certains éléments d’une liste triée on peut stocker plus d’informations.
http://www.di.unipi.it/~grossi/PAPERS/jfocs04.pdf
(c’est quoi ce forum consacré à l’informatique théorique ?)
@mmm:
Non, l’ordinateur n’a pas créé d’information car son fonctionnement est purement déterministe.
Pour que l’ordinateur crée de l’information, il faut lui adjoindre un générateur de nombre aléatoires.
Il faut aussi remarquer que l’information au sens informatique n’est pas celle au sens usuel: il y a beaucoup plus d’information dans:
« tBx e’!i/$18yhaOO-2EbqmhV^Sgyo7]Ys]=bykL5]Z~( »
que dans
« La Suisse est un pays de 7.7 millions d’habitants ».
En fait, une bonne part de l’informatique a pour objet de détruire de l’information, une bonne part de ce qui rentre dans un ordinateur étant totalement inutile. Enfin répéter sur un support (écran ou son) requiert en général de détruire l’information qui y était préalablement affichée.
En ce sens, l’ordinateur a la même tâche que beaucoup d’autres machines humaines, à savoir réduire une entropie (entropie=+/-information) d’un système en augmentant celle du reste de l’univers.
mmm…
« » »
l’informatique détruit toujours l’information.
« » »
Question:
j’ai une entrée x est une liste Y = [y0..yN]
je calcule, via un algorithme donnée la distance entre x et tout les éléments de Y, pour trouver l’élément le plus proche (indiqué comme yx).
Oui le fait que yx est le plus proche est une vérité qui existait avant de faire le calcul. Mais avoir calculé le résultat donne de l’information en plus pour l’utilisateur, sans avoir ajouté ou modifié les données. Dans ce cas, « l’informatique n’a-t-elle pas créé de l’information » ?