Google trie 1 PetaByte de données !

Pour trier un jeu de 72 cartes, je prends une carte de mon jeu mélangé, et je la pose sur la table. J’en prends une seconde, et je la place sur la table avant ou après la première selon l’ordre que je souhaite. La troisième carte peut aller avant ou après les deux premières, ou être insérée entre les précédentes, et ainsi de suite jusqu’à ce que toutes les cartes soient triées dans l’ordre sur la table, ce qui me prend un peu plus d’une minute.

Un TeraByte pour commencer

Dans le même temps de 68 secondes, Google vient d’arriver à trier 10 milliards de « cartes », améliorant d’un facteur 3 le record de Yahoo! obtenu plus tôt cette année. Suivant les règles du  « terabyte sort benchmark » proposé par Jim Gray en 1998, les cartes contenaient 100 bytes, ce qui représente au total un TeraByte, l’équivalent, grosso-modo, d’un annuaire qui inclurait tous les habitants de la planète.

Un TeraByte, c’est la capacité d’un gros disque dur actuel, mais on ne peut y lire ou écrire « que » 300 MegaByte par seconde : il faudrait au mieux une heure pour lire les donner à trier dans une mémoire de 1000 GigaByte (qui n’existe pas…) et une autre heure pour réécrire la liste triée, sans compter le temps du tri proprement dit . Google a donc utilisé 1000 ordinateurs, et au moins autant de disques durs formant une partie du « Google File System » [1], le gigantesque système de stockage de Google.

Trions en parallèle

Mais comment trier les mêmes données à plusieurs? Reprenons le jeu de 72 cartes et divisions le en 2 tas de 36 cartes mélangées, un pour toi, un pour moi. Nous pourrions placer nos cartes sur une seule ligne sur la table et espérer le faire 2 fois plus vite, mais problème peut survenir si nous voulons simultanément insérer nos cartes au même endroit : comment les placer dans le bon ordre dans ce cas ?  Soit on doit alors comparer nos deux cartes et éventuellement les intervertir avant de les insérer, soit on doit convenir d’insérer les cartes à tour de rôle, ce qui ralentit considérablement l’opération. Avec 1000 ordinateurs, on ne va pas s’en sortir beaucoup mieux car c’est visiblement l’accès à la table (=mémoire), unique, qui forme un goulot d’étranglement : pas efficace.

Une autre approche serait que je trie mes 36 cartes et toi tes 36 cartes indépendamment, puis que nous réunissions nos deux piles triées, ce qui est très rapide : je pose mes cartes une à une tant qu’elles viennent avant celle que je vois sur le haut de ta pile, et quand je ne peux plus en poser, tu poses les tiennes tant qu’elles viennent avant celle que je ne pouvais plus poser etc.

On peut faire même mieux en échangeant astucieusement nos cartes plutôt que de reformer une seule pile. Si je trie les carreaux et coeur, et toi les trèfles et pique, plus besoin de reformer une pile unique à la fin : commençons par nous échanger les cartes qui n’ont pas la bonne couleur, puis trions nos tas chacun sur notre table, et voilà !

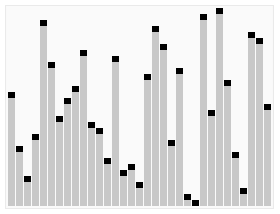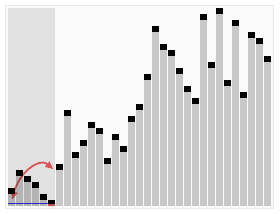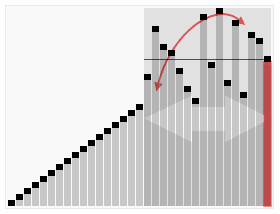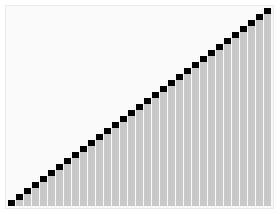
QuickSort

Voilà qui ressemble furieusement à l’algorithme de tri rapide « Quick Sort » illustré ci-contre : on commence par échanger les données plus grande qu’un pivot (seuil bleu) de la première moitié contre celles plus petites que le seuil de la 2ème moitié. Puis on peut répéter l’opération entre le premier quart et le second d’une part, et le 3^ème et le 4^ème d’autre part, et ainsi de suite. Si on a un nombre de données qui est une puissance de 2, on peut tout trier par simples échanges, et si on dispose aussi d’un nombre de processeurs qui soit une puissance de deux, on peut répartir le travail très efficacement. A quelques variations près, c’est cet algorithme [3] qui est utilisé pour trier de très grosses quantités de données.

MapReduce

S’il y a un sujet sur lesquel j’aurais du me documenter avant d’aller voir Google, c’est MapReduce [2]. Le principe est tout simple :

• le programmeur écrit :
  • une fonction « map » qui sera appliquée à chaque donnée et produira un résultat intermédiaire
  • une fonction « reduce » qui regroupera les résultats intermédiaires de « map » pour produire le résultat final
• on donne ces deux fonctions à MapReduce, qui se charge de les exécuter de façon efficace sur beaucoup de donnée sur beaucoup de disques durs et beaucoup d’ordinateurs.

Le MapReduce de Google contient en fait un algorithme de partitionnement qui répartir les résultats des « map » sur les « reduce », et un algorithme de tri incorporé à la partie « Reduce », car les fonctions « reduce » peuvent presque toujours être rendues plus efficaces si leurs données sont triées. De ce fait, il semblerait que le record du tri ait été obtenu avec une fonction « map » triviale, et une « reduce » qui ne l’est pas moins!

MapReduce est probablement la plus géniale idée des ingénieurs de Google, et une contribution majeure à l’informatique du futur. Le code n’est pas public, mais tout le monde peut l’utiliser.  D’autre part la fondation Apache a un équivalent OpenSource, qui se base sur Hadoop, leur équivalent du Google File System. C’est en utilisant ce système + 1000 lignes de Java seulement que Yahoo! a pu trier le TeraByte en 209 secondes [4]. 3x moins bien que Google, c’est quand même pas mal du tout…

Pour en savoir plus sur MapReduce vous pouvez lire la référence [2], et/ou :

• regarder cette vidéo
• consulter ces slides de présentation, plus techniques, avec exemple de code [2] et performances

Et un PetaByte, un !

Une fois qu’on a un stockage distribué (GFS), un système de traitement parallèle massif (MapReduce) et quelques milliers d’ordinateurs, pourquoi se limiter à trier un TeraByte ? Comme ils le disent dans leur annonce, Google était « curieux de voir ce qui arrive si on essaie avec un PetaByte ». 1000x plus quoi. Juste pour voir…

Ca a pris 6 heures et 2 minutes, soit 21720 secondes sur 4000 ordinateurs. Ramené au même nombre d’ordinateurs, ça a donc pris « seulement » 1277x plus de temps pour trier 1000x plus de données. C’est assez efficace si l’on considère que la complexité d’un algorithme comme QuickSort est O(N.log N) : sur un seul ordinateur, trier 1000x plus de données prend théoriquement 1000×10 = 10’000x plus de temps. Mais en répartissant le tri sur 4 fois plus d’ordinateurs, on divise ce temps par 4 et en plus on divise par 4 la taille des données : on devrait se retrouver avec 250×8/4 = environ 500x plus de temps. Un facteur 1277 c’peut sembler nettement plus, mais c’est normal en raison des communications supplémentaires entre les ordinateurs.

Le tri du PetaByte pose une autre problème intéressant : les données étaient réparties sur 48’000 disques durs et statistiquement, en 6 heures de calcul, au moins un des disques tombe en panne [7] ! Il faut donc que les données triées soient redondantes pour que l’on puisse remplacer le disque fautif sans interrompre l’exécution du tri, ce qui illustre une autre fonctionnalité remarquable du Google File System …

Et après ?

Peu de groupes au monde disposent d’assez de ressources pour tenter de faire mieux que Google. Mais heureusement, les records de tri sont ouverts à d’autres catégories:

• la catégorie « penny » consiste à trier le plus de nombres possibles pour un « cout » d’un penny, environ 1.3 centimes d’Euro. Le record actuel a été obtenu sur un PC doté d’un AMD 64 sous Linux, mais surtout de 4 disques dur SATA, qui a trié 1’812’000 enregistrements de 100 bytes en 2.408 secondes
• la catégorie « Minute » limite le temps de calcul à 60 secondes. Une machine parallèle du MIT a trié 2.140 Milliards d’enregistrements de 100 bytes toujours en 2007.
• la catégorie « JouleSort » me semble plus intéressante au niveau du matériel que du logiciel : il s’agit de trier un maximum de nombres par Joule d’énergie consommée par l’ordinateur. Le record appartient à un ordinateur portable utilisant un processeur intel Mobile Core 2 Duo doté de 13 (!) disques durs, et qui trie environ 11’300 enregistrements par Joule [7]. Si les machines de Google avaient la même efficacité énergiétique, le tri du PetyBytes aurait consommé 0.885 GigaJoule, soit 246KWh. Répartis sur 6 jours, ça donne une puissance de 1.7 KW seulement. Un petit radiateur. Mais avec 4000 gros PC et 48’000 disques durs, Google est probablemet autour de 20x plus.

Et les spaghetti dans tout ça ?

Je ne peux me résoudre à terminer un article sur le tri sans parler du tri par les spaghetti qui m’avait émerveillé il y a près de 25 ans déjà [9].

Comme on l’a vu plus haut, les meilleurs algorithmes de tri existant ont une complexité O(N.Log N) : le temps de calcul augmente plus vite que le nombre des données, et malgré quelques progrès dus à la parallélisation, il n’existe pas de tri informatique général* en O(N).

Pourtant, des spaghettis pourraient réussir là où les superordinateurs patinent :

1. on coupe un spaghetti à une longueur représentant le premier enregistrement à trier ramené à un nombre. On coupe un autre spaghetti à la longueur du second nombre, et ainsi de suite pour tous les nombres, et en un temps O(N) on obtient N spaghettis.
2. on pose verticalement la botte de spaghettis sur une table plane de façon à tasser tous les spaghettis contre la table. Ceci prend un temps constant, très court et indépendant de N et ne compte donc pas dans la complexité globale
3. En posant une planche enduite de colle sur la botte, on extrait le spaghetti le plus long, on le mesure, on retransforme le nombre en une donnée qu’on écrit au bas de la liste triée et on recommence N fois, pour chaque spaghetti.

Voilà, les spaghettis permettent de trier nos enregistrements en un temps proportionnel à N ! Trier 1000x plus de spaghettis prendra exactement 1000x plus de temps. En fait, si on disposait d’une machine capable de couper puis de mesurer 150 millions de spaghetti à la seconde, elle aurait égalé la machine de Google sur le TeraByte, et l’aurait battu sur le PetaByte, en 18.8 heures seulement 🙂

Plus sérieusement, si on a besoin de trier des objets physiques (des grains de sable, des protéines, des ADN ?), il pourrait être intéressant de ne pas oublier la leçon des spaghetti : certains dispositifs physiques peuvent être plus rapides que les plus puissants ordinateurs [10]

Références

1. Sanjay Ghemawat, Howard Gobioff, and Shun-Tak Leung « The Google File System« , 19th ACM Symposium on Operating Systems Principles, Lake George, NY, October, 2003.
2. Jeffrey Dean and Sanjay Ghemawat, « MapReduce: Simplified Data Processing on Large Clusters » OSDI’04: Sixth Symposium on Operating System Design and Implementation,
   San Francisco, CA, December, 2004.
3. Jim Wyllie, « SPsort: How to Sort a Terabyte Quickly« , IBM, February 4, 1999
4. Owen O’Malley, « TeraByte Sort on Apache Hadoop« , Yahoo!, May 2008
5. Sort Benchmark Home Page : records de tri de données depuis 1987
6. “A Measure of Transaction Processing Power“  Datamation, V 31.7, April 1985, pp 112-118.
7. Eduardo Pinheiro, Wolf-Dietrich Weber and Luiz André Barroso, « Failure Trends in a Large Disk Drive Population« , Google Inc. Proceedings of the 5th USENIX Conference on File and Storage Technologies (FAST’07), February 2007.
8. Suzanne Rivoire et al. « JouleSort: A Balanced Energy-Efficiency Benchmark« ,SIGMOD’07, June 11–14, 2007, Beijing, China
9. Dewdney, A. K. »On the spaghetti computer and other analog gadgets for problem solving », Scientific American, (June 1984), 250 (6): 19-26
10. Niall Murphy et al. « Implementations of a model of physical sorting« , International Journal of Unconventional Computing,2008, Vol 4 nr 1, pages 3-12

Note* : il existe des algorithmes de tri de complexité linéaire sur des données satisfaisant certaines hypothèses, comme Hervé me l’a fait remarquer dans un commentaire