Cette question est cruciale pour la conception de balles de golf, mais aussi pour certaines fraises, de boules à facettes de discothèque. Et une fois qu’on sait y répondre pour une sphère, on peut s’attaquer aux surfaces quelconques, par exemple pour recouvrir de diamants une montre ou un bijou …
D’abord, il faut définir ce qu’on appelle « régulièrement ». Plusieurs définitions sont possibles, chacune correspondant à un problème et à des méthodes distinctes pour le résoudre :
- le « covering » consiste à recouvrir complètement la sphère par des disques de même rayon, appelé « rayon de couverture » (« covering radius » en anglais). Les disques sont donc forcés de se recouvrir partiellement. Mathématiquement on « minimise la distance maximale ‘d’ de tout point de la sphère à son voisin le plus proche ». (définition corrigée grâce à Anton Sherwood )
- le « packing » est une petite nuance consistant à « maximiser la distance minimale entre les points ». Autrement dit, l’optimum est atteint lorsqu’on ne peut plus écarter les deux points les plus proches car l’un se rapprocherait davantage d’un troisième point.
- le « convex hull » consiste à maximiser le volume du solide convexe défini par les N sommets
- la « minimisation de l’énergie potentielle » consiste à minimiser la somme de l’énergie qui serait accumulée dans des ressorts liant chaque paire de points. Les ressorts peuvent être soit linéaire (d’ordre 1), soit quadratiques (ordre 2) ce qui correspond au cas de la répulsion électrostatique de points supposés chargés électriquement.
Intuitivement on « sent » que certaines de ces méthodes devraient donner les mêmes résultats, mais ce n’est pas le cas sauf dans des cas très particuliers.
Solutions exactes
Le seul problème pour lequel il existe des solutions exactes est le « covering » car en 1943 (seulement….) Fejes Tóth a trouvé la borne du « rayon de couverture » d en fonction de N (voir ici) . Il a ainsi enfin été prouvé que :
- pour N=4, la disposition optimale correspond aux sommets d’un tétraèdre régulier
- pour N=6, aux sommets d’un octaèdre
- pour N=8, ce ne sont pas les sommets d’un cube, mais de l'antiprisme carré
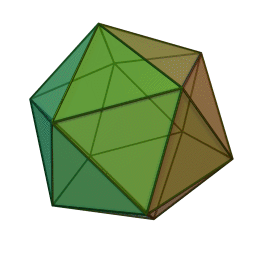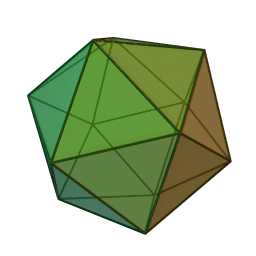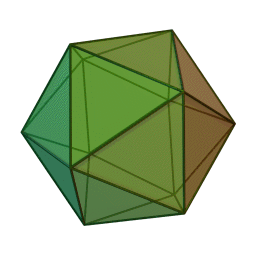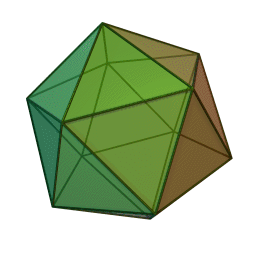
- pour N=12, ce sont les sommets d’un icosaèdre. L’icosaèdre (ci-contre) est formé de 20 triangles équilatéraux égaux
- pour N=20, on peut donc projeter sur la sphère les centres des 20 faces de l’icosaèdre, ce qui va avoir de l’importance dans la suite
de plus :
- pour N=5, on ne peut pas faire mieux que d’enlever un point de l’octaèdre (N=6)
- pour N=7, il faut dessiner sur la sphère des triangles sphériques d’angle = 80° (étonnant, 2/9èmes de 360° …)
- pour N=9, les triangles sphériques doivent avoir un angle tel que cos(angle)=1/4
et c’est tout pour les solutions démontrées comme optimales ! Les solutions du « packing » et du « convex hull » pour les mêmes valeurs de N semblent être les mêmes, mais on ne l’a jamais prouvé formellement !
Pour toutes les autres valeurs de N, les solutions ne peuvent pas être construites géométriquement, mais seulement par des méthodes approximatives.
Solutions icosahédriques
 Pour certaines valeurs de N, on peut construire de « jolis » arrangements « presque » optimaux en utilisant l’intéressante propriété de l’icosaèdre d’être optimal et d’avoir des faces triangulaires équilatérales. En subdivisant une face (qui est un triangle équilatéral) en plus petits triangles équilatéraux puis en projetant les sommets sur la sphère, et en appliquant la « symétrie icosahédrale » consistant à recopier ces points pour chacune des 20 faces de l’icosahèdre, on obtient les formes en « géode » bien connues dans la construction
Pour certaines valeurs de N, on peut construire de « jolis » arrangements « presque » optimaux en utilisant l’intéressante propriété de l’icosaèdre d’être optimal et d’avoir des faces triangulaires équilatérales. En subdivisant une face (qui est un triangle équilatéral) en plus petits triangles équilatéraux puis en projetant les sommets sur la sphère, et en appliquant la « symétrie icosahédrale » consistant à recopier ces points pour chacune des 20 faces de l’icosahèdre, on obtient les formes en « géode » bien connues dans la construction
La page Tables of Spherical Codes with Icosahedral Symmetry de R. H. Hardin, N. J. A. Sloane and W. D. Smith fournit ce type de solutions pour N=60, 72, 80, 90 … 78032. (l’applet n’a plus l’air de marcher, mais il y a du code C permettant de générer les solutions)
Les balles de golf
Pour des raisons aérodynamiques, les balles de golf ont entre 300 et 450 petites cavités (« dimples » en anglais). C’est le règlement du golf qui impose qui doivent être réparties les plus régulièrement possible, alors que la stabilisation de la balle en vol pourrait être mieux assurée par une balle du type « polara », ayant des cavités différentes le long d’un équateur.
La plupart des balles de golf existantes sont donc construites par symétrie icosahédrale, en veillant à ce qu’il n’y ait pas de cavité le long d’une ligne pour permettre la réalisation de moules « simples ». Comme on le voit ci-dessous, on peut remplir les faces triangulaires de l’icosaèdre de nombreuses façons, et même jouer sur la dimension des « dimples » pour tenter de compenser des irrégularités :
 Ce site vend un CD contenant plus de 800 brevets relatifs aux balles de golf, la plupart relatifs à la disposition des dimples (images ci-contre) ! Ceci prouve qu’il n’existe pas un N clairement optimal, ni une façon optimale de répartir les points.
Ce site vend un CD contenant plus de 800 brevets relatifs aux balles de golf, la plupart relatifs à la disposition des dimples (images ci-contre) ! Ceci prouve qu’il n’existe pas un N clairement optimal, ni une façon optimale de répartir les points.
Méthodes « empiriques »
Cette page présente 3 méthodes qui permettent de placer très rapidement des points à une distance à peu près égale à d les uns des autres, mais il n’est pas garanti que l’on arrive à en placer le nombre N souhaité. Il faut apparemment faire plusieurs essais avec des N’>N pour obtenir éventuellement un nombre N précis. Ces méthodes sont illustrées ci dessous pour N=124, qui ne permet pas une symétrie icosahédrique:
 Une méthode proposée par Dave Rusin consiste à placer les points le long de l’équateur (ou de chaque côté de l’équateur) à une distance d les uns des autres, puis le long de « latitudes » séparées d’une distance d. Une méthode proposée par Dave Rusin consiste à placer les points le long de l’équateur (ou de chaque côté de l’équateur) à une distance d les uns des autres, puis le long de « latitudes » séparées d’une distance d. |
 la méthode de Saff et Kuijlaars est décrite par un petit algorithme dans une FAQ de maths : elle consiste à placer les points à distance d les uns des autres le long d’une spirale qui va d’un pôle de la sphère à l’autre. la méthode de Saff et Kuijlaars est décrite par un petit algorithme dans une FAQ de maths : elle consiste à placer les points à distance d les uns des autres le long d’une spirale qui va d’un pôle de la sphère à l’autre. |
 une variante de la précédente basée sur une spirale utilisant le nombre d’or pour éviter toute régularité apparente. une variante de la précédente basée sur une spirale utilisant le nombre d’or pour éviter toute régularité apparente.Je n’ai pas tout compris, mais cette méthode donne le meilleur résultat « visuel » |
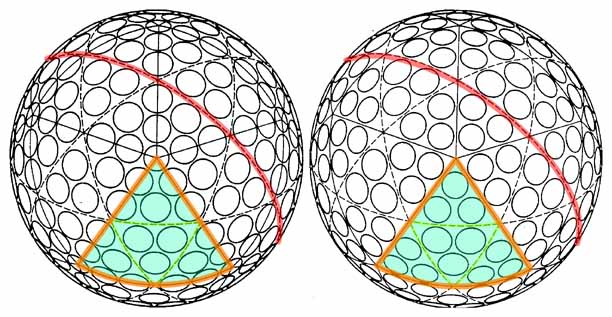
La couleur rouge permet de comparer les méthodes : les disques sont réduits jusqu’à être tangents entre eux, et on colore en rouge la différence entre chaque diamètre et le diamètre le plus faible. On constate que la première méthode est systématiquement meilleure que les 2 autres, mais on « voit » qu’elle est encore loin de l’optimum
Référence : page de liens sur le sujet « How can I arrange N points evenly on a sphere? »




11 commentaires sur “comment placer N points “régulièrement” sur une sphère ?”
Trouvé un bout de code Python qui implante la méthode « spirale d’or » : https://gist.github.com/goulu/ebbe9a41b34a6730bc54
Chouette article sur l’aérodynamique des balles de golf ici : http://www.voyagesaucoeurdelascience.fr/le-secret-des-alvoles-des-balles-de-golf/
il en reste un lien à refaire
merci pour cet article « en français », j’ai contribué( avec deux autres professeurs) à la résolution de ce problème à l’aide de la « minimisation de l’énergie potentielle ». Ci joint les liens mes articles en ce sujet.
http://www.ijser.org/researchpaper%5CEnergy-Minimization-of-Point-Charges-on-a-Sphere-with-a-Spectral-Projected-Gradient-Method.pdf
http://www.m-hikari.com/ams/ams-2012/ams-29-32-2012/lakhbabAMS29-32-2012.pdf
J’ai déménagé d’ogre.nu à bendwavy.org, domaine moins cher.
Merci Anton. J’ai pu diminuer de 4 le nombre de liens cassés 🙂
Un autre lien intéressant sur le sujet est cette page, avec un programme pour tester divers algorithmes :
http://particules.sectionpc.info/
Anton your french is perfect! Thank you for pointing my mistakes out, I corrected the definition. As you will see in a next article, this was just an introduction to the area, as I am working on an add-in for SolidWorks (a 3D CAD) to help jewelers to cover any surface with expensive stones…
Merci de m’avoir cité. (Mon français est bien rouillé, donc j’espère qu’on me signalera si je m’égare en absurdités.)
La définition de covering est inexacte: il s’agit de couvrir toute la sphère par des disques, en tolérant les chevauchements inévitables. On veut bâtir par example N hôpitaux sur une planète, plaçés pour minimiser la distance qu’une ambulance devra voyager en pire cas. (Le problème se surnomme parfois celui des « dictateurs amicaux »; le problème packing, des « dictateurs hostiles ».)
Dans mes dessins, les anneaux rouges montrent l’inégalité dans la solution: le diamètre du cercle blanc est la moindre distance entre les voisins (cas qui se trouve généralement près des « pôles »), et le diamètre du cercle rouge est la distance entre chaque nœud et son propre voisin. Un « packing » optimal peut bien avoir quelques nœuds un peu libres (« rattlers », cliqueteux), qui auraient de larges anneaux rouges.
Selon le méthode Rusin, le nombre de bandes peut être pair; il n’y aura donc pas de nœuds sur l’équateur.
Cela permet aussi de calculer l’angle des liaisons entre les molécules par exemple.