Répartition proportionnelle

Voici un petit problème qui se présente assez fréquemment sous diverses formes, et pour lequel j’ai été surpris de ne pas trouver de solution bien documentée.

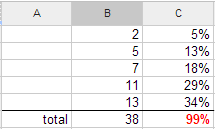
Le cas le plus simple apparaît souvent dans les tableurs : en calculant des pourcentages arrondis, le total ne fait parfois pas 100%. En effet, rien ne garantit que les arrondis « vers le haut » compensent ceux « vers le bas ». Autrement dit, une somme d’arrondis n’est pas égale à la somme arrondie.

Autre exemple assez différent en apparence. Un berger veut répartir ses 1548 moutons sur sa parcelle carrée d’un hectare où il veut faire paître a moutons, son parc rond de π hectares qui peut en accueillir b, et les c restants sur la parcelle louée à son voisin le père Néper, qui fait e hectares, de manière à ce que chaque mouton ait la même surface à brouter. Sur les conseils de l’instituteur du village, il commence par écrire la petite équation a.(1+π+e) = 1548 pour obtenir a = 225.66 puis b=708.93 et c=613.41, mais ensuite, comment arrondir chacun de ces nombres vers le haut ou le bas de façon à obtenir exactement un total de 1548 et que les rapports b/a et c/a restent respectivement proches de π et de e ?

C’est en planchant sur un problème de ce type que m’est venue une idée : utiliser une méthode du scrutin proportionnel plurinominal !

Certains parlements comme le Conseil National (Suisse) sont élus à la « proportionnelle par liste » : le nombre de sièges étant fixé, on commence par répartir ces sièges entre les partis proportionnellement aux nombre de listes portant l’entête d’un parti choisies par les électeurs. Dans une deuxième phase, les n candidats ayant reçu le plus de voix de chaque parti sont élus aux n sièges attribués à leur parti, mais ceci n’est pas le sujet ici.

La phase de répartition des sièges entre partis rencontre exactement les difficultés liées aux arrondis mentionnées plus haut, et comme l’enjeu est d’importance politique, le problème a été non seulement étudié depuis longtemps, mais les solutions sont mêmes formalisées dans les lois régissant le système électoral de bon nombre d’Etats (voir [1] par exemple). Le hic, c’est qu’il n’y a pas une seule solution définitive mais plusieurs, chacune avec ses avantages et inconvénients.

La « méthode de Hare » est la plus simple des méthodes dites « du plus fort reste ». On commence par calculer un « quotient électoral » en divisant le nombre total de votes valides par le nombre de sièges à pourvoir. Dans le cas d’une élection on obtient en principe un nombre assez grand, mais pour les prés de notre berger, on a:
q = (1+π+e)/1548 = 0.004431 , ce qui n’est autre que la surface à brouter par chaque mouton.

Puis on effectue la division euclidienne (ou entière) du nombre de votes obtenus par chaque parti par ce nombre q. Peu importe que dans notre cas, les votes soient remplacés par des nombres réels, l’important est que l’on souhaite diviser un nombre entier en entiers suivant cette proportion.

On commence par ne considérer que les quotients des divisions entières (notées // en Python) et assigner
a = 1//q = 225, b = π//q = 708 et c = e//q = 613 moutons aux trois champs. Mais a+b+c ne totalisant que 1546 moutons, il reste à attribuer les moutons restants aux deux « plus fort restes » des divisions entières. Dans notre cas, 1-a.q = 0.0029, π-b.q = 0.0041 et e-c.q = 0.0018, donc on alloue un mouton de plus aux champs b et a pour obtenir finalement a=226, b=709 et c=613.

La méthode de Hare souffre d’un défaut appelé paradoxe de l’Alabama : le fait d’augmenter de 1 le nombre de sièges/moutons peut dans certains cas faire diminuer de 1 le nombre alloué à l’un des partis/prés, ce qui est illogique. De plus, la méthode de Hare avantage les petits partis qui pourraient gagner leur seul élu au plus fort reste. Les grands partis pourraient même être tentés de déposer plusieurs listes apparentées pour gagner des sièges, c’est pourquoi les législations introduisent souvent un quorum ou « seuil de représentativité » sous la forme d’un pourcentage minimum de votes à atteindre pour qu’une liste soit prise en considération*.

On peut diminuer la probabilité d’apparition de ces défauts à l’aide d’une astuce due à Eduard Hagenbach-Bischoff (1833-1910), scientifique suisse qui proposa de calculer le « quotient électoral » en divisant le nombre total de votes valides par le nombre de sièges à pourvoir augmenté de 1. Le « quotient de Hagenbach-Bischoff » vaut dans notre cas  q = (1+π+e)/(1548+1) = 0.004429. La différence par rapport à la méthode de Hare est très faible, mais suffit à répartir 225+709+613=1547 moutons du premier coup, n’en laissant qu’un à attribuer au parti/pré a puisqu’il présente le reste de division le plus élevé, ce qui nous donne le même résultat qu’Hare dans ce cas précis : a=226, b=709 et c=613

Il existe d’autres variantes de quotients électoraux (de Droop, de Imperiali), ainsi que des méthodes dites « de la plus forte moyenne » dans lesquelles on attribue un des sièges restants au parti dont la moyenne des votes/sièges est la plus élevée, puis on recommence tous les calculs jusqu’à ce que tous les postes soient attribués. L’une des plus utilisées, y compris en France pour les élections au Parlement Européen, est est la méthode du belge D’Hondt, connue pour avantager les grands partis, alors que celle du français Sainte-Laguë qui représente mieux les petits partis est plutôt utilisée en Allemagne et au Nord de l’Europe…

Mais revenons à nos moutons : la méthode Hare suffit parfaitement à mon problème, mais le quotient de Hagenbach-Bischoff ajoute un petit plus de science helvétique qui me plaît assez…

J’ai donc codé la méthode du plus fort reste dans un tableur Google exportable en Excel. Trois onglets résolvent le cas des 1548 moutons, celui des pourcentages du début de l’article, et celui du scrutin proportionnel utilisé comme exemple dans la page Wikipédia et qui donne des résultats différents selon le quotient électoral ( Hare, Hagenbach-Bischoff ou Imperiali) choisi. Pour les curieux, la cellule F1 utilise la fonction Excel LARGE, GRANDE.VALEUR en français pour obtenir la n-ième plus grande valeur des restes calculés dans la colonne E, où n est le nombre de sièges restant à attribuer. Ensuite un simple test permet de déterminer dans la colonne F si un siège/mouton/pourcent doit être ajouté.

Le « bug connu », c’est qu’en cas d’égalité des restes il se pourrait qu’on en ajoute trop, mais je ne sais pas trop comment empêcher ceci en Excel sans macro… Par contre ce problème est évité dans la fonction Python que j’ai réalisée pour mon application:

Si vous trouvez ce code utile ou intéressant, vous pouvez voter pour ma réponse à une question sur StackOverflow, ça me fera une voix de plus en attendant un siège …

Note : * à mon humble avis le quorum devrait donc être approximativement égal à 1 / le nombre de sièges à pourvoir, donc autour de 1% plutôt que 5 ou 7% dans certains parlements…

Références:

1. « Loi fédérale sur les droits politiques, Art 40« 
2. David Madore « Élections à la proportionnelle : illustrations« , 10 juin 2009